网讯:
摘要 针对不合理虚拟惯性控制参数引发的直流微电网高频振荡失稳问题,提出了低通滤波器等效建模方法,建立了直流微电网的降阶模型及其电压闭环传递函数。从保证直流微电网小扰动稳定性角度出发,定义了以下垂系数和低通滤波控制带宽为参数空间的虚拟惯性参数可行域概念。基于电压闭环传递函数得到的零极点,提出了虚拟惯性参数可行域求解方法,该可行域为直流微电网的虚拟惯性控制参数设计提供了切实可行的指导依据。最后,利用PLECS软件搭建了基于开关模型的直流微电网仿真算例,多组仿真结果均验证了降阶模型和虚拟惯性控制参数可行域的有效性。
1 直流微电网的高频振荡失稳问题
1.1 直流微电网拓扑
典型直流微电网拓扑如图1所示,该直流微电网主要由n台DC/DC变换器、n条直流线路和1个等效恒功率负荷等构成。其中,Lsn、Csn和Rsn分别为第n台DC/DC变换器的滤波电感、滤波电容和滤波电阻;Usn和Isn分别为第n台DC/DC变换器的输入电压和滤波电感电流;UOn和IOn分别为第n台DC/DC变换器的输出电压和输出电流;Kpin和Kiin分别为第n个电流控制器的比例系数和积分系数;Kpun和Kiun分别为第n个电压控制器的比例系数和积分系数;Dsn为第n台DC/DC变换器的占空比;Urefn和Kdn分别为第n台DC/DC变换器的电压参考值和下垂系数;ωfn为第n台DC/DC变换器的低通滤波器控制带宽;s为拉普拉斯算子;Lln和Rln分别为第n条直流线路的线路电感和线路电阻;Irn和ICsn分别为第n台DC/DC变换器的滤波电感电流参考值和滤波电容电流;Ccpl、Icpl和Pcpl分别为恒功率负荷的输入滤波电容、电流和功率,U为直流母线电压。
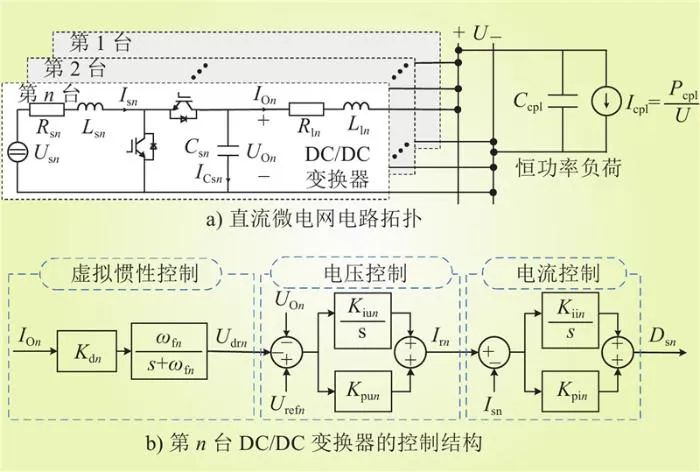
图1 直流微电网拓扑
Fig.1 Topology of the DC microgrid
1.2 两种典型虚拟惯性控制策略
为增强直流微电网的虚拟惯性,通常会采用图2所示的2种典型虚拟惯性控制策略:基于低通滤波器和基于类虚拟同步发电机的虚拟惯性控制策略。
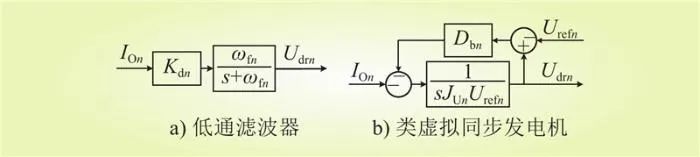
图2 2种典型虚拟惯性控制策略
Fig.2 Two typical virtual inertia control strategies
上述2种典型虚拟惯性控制策略之间可以相互转化,其关系式为
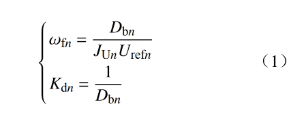
式中:JUn和Dbn分别为采用类虚拟同步发电机控制的第n台DC/DC变换器的转动惯量和阻尼系数。
为方便起见,本文将以基于低通滤波器的虚拟惯性控制为例开展理论研究工作。
1.3 高频振荡失稳问题
以文献[10]中的直流微电网为研究对象(2台DC/DC变换器的电压比例系数均为1,其余参数均与文献[10]保持一致),利用PLECS软件搭建其开关模型。在0.8 s时,恒功率负荷的功率从0.7 kW突增至1.4 kW,直流微电网的直流母线电压时域仿真结果如图3所示。可以看出,直流母线电压出现了振荡频率约为476 Hz(振荡周期约为0.0021s)的高频振荡失稳现象。
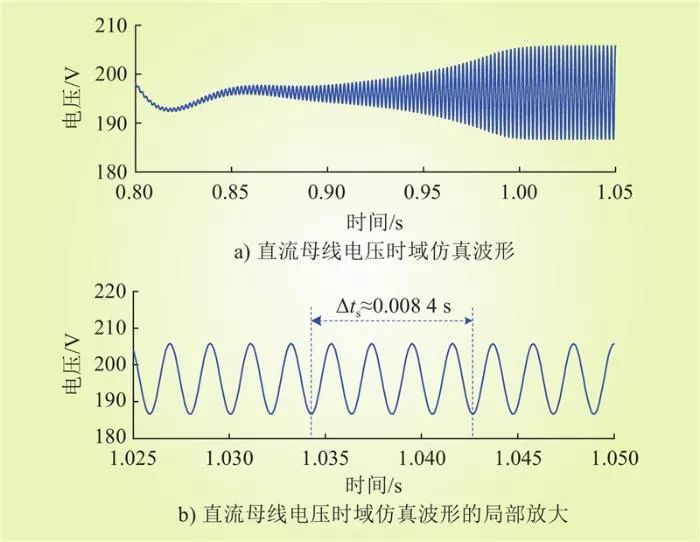
图3 直流微电网的高频振荡仿真结果
Fig.3 Simulation results of high-frequency oscillations in DC microgrid
2 基于降阶模型的虚拟惯性参数可行域
2.1 直流微电网的降阶模型
为解决高阶模型造成的直流微电网小扰动稳定性分析难题,本文提出了低通滤波器等效建模方法。图1直流微电网的全阶模型阶数为6n+1阶,利用该方法对直流微电网进行降阶处理,得到阶数为7阶的降阶模型,如图4所示。图中,Rs、Ls和Cs分别为降阶模型的滤波电阻、滤波电感和滤波电容;Us和Is分别为降阶模型的输入电压和滤波电感电流;UO和IO分别为降阶模型的输出电压和输出电流;ICs和Ir分别为降阶模型的滤波电容电流和滤波电感电流参考值;Kpi和Kii分别为降阶模型的电流比例系数和电流积分系数;Kpu和Kiu分别为降阶模型的电压比例系数和电压积分系数;Ds为降阶模型的占空比;Uref和Kd分别为降阶模型的电压参考值和下垂系数;ωf为降阶模型的低通滤波器控制带宽;Ll和Rl分别为等效直流线路的线路电感和线路电阻;Ur为降阶模型的电压参考信号。
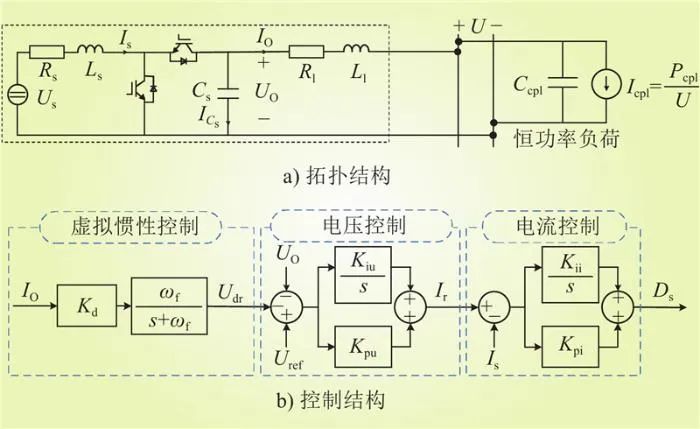
图4 降阶模型拓扑
Fig.4 Topology of the reduced-order model
2.1.1 基于低通滤波器的虚拟惯性控制降阶建模
由图1可知,第n台DC/DC变换器的虚拟惯性控制表达式为
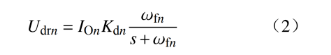
由于直流微电网中DC/DC变换器及直流线路均来自同一厂家,电路参数和控制参数均相同,即
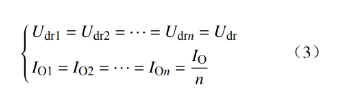
进而,直流微电网中n个基于低通滤波器的虚拟惯性控制环节可以等效为
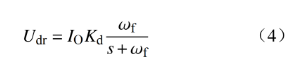
联立式(2)、(3)和(4),可得
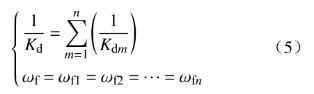
至此,图1直流微电网中的n阶虚拟惯性控制环节,可以等效为图4降阶模型中的1阶虚拟惯性控制环节。
2.1.2 电压控制和电流控制降阶建模
根据文献[24],直流微电网中n个电压控制器(或电流控制器)可以等效为1个电压控制器(或电流控制器),即
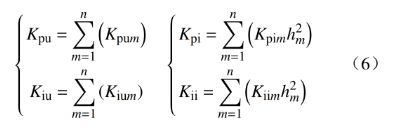

2.1.3 降阶模型的有效性验证
相同扰动情况下,降阶模型的时域仿真结果如图5所示。由图5可知,直流微电网与其降阶模型的直流母线电压时域仿真结果基本一致,验证了本文所提低通滤波器等效建模方法的有效性。
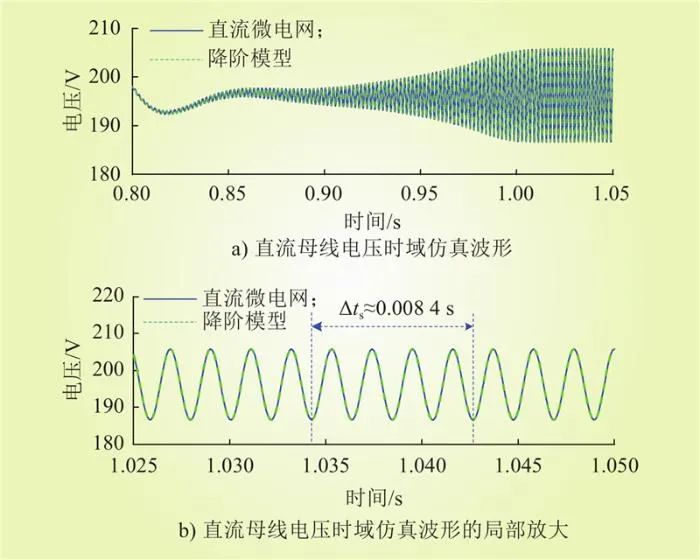
图5 降阶模型的高频振荡仿真结果
Fig.5 Simulation results of high-frequency oscillations in the reduced-order model
2.2 降阶模型的电压闭环传递函数
2.2.1 降阶模型的电压闭环传递函数理论推导
对图4所示的降阶模型进行线性化处理,可得到电压闭环传递函数Guiu(s)为
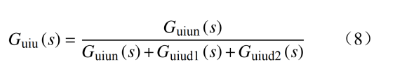
式中:Guiun(s)、Guid1(s)和Guid2(s)分别为传递函数Guiu(s)的分子、第1个分母和第2个分母传递函数,具体表达式分别为

式中:Rcpl为等效电阻;Gudld(s)和Gudln(s)分别为传递函数Gud(s)的分子和分母。
2.2.2 高频振荡失稳问题的理论分析
传递函数Gud(s)和Guiu(s)的频域响应曲线如图6所示,将对图5中的高频振荡失稳现象进行理论解释。传递函数Gud(s)在频率485 Hz处存在一个高频振荡尖峰。结合图4可知,该高频振荡尖峰的LC振荡环节由恒功率负荷的输入滤波电容Ccpl与等效线路阻抗Rl/Ll共同构成。由图6可知,传递函数Guiu(s)在振荡频率485 Hz处也存在一个高频振荡尖峰。据此可推断出,在现有虚拟惯性参数情况下,低通滤波器未能有效抑制该高频振荡尖峰。
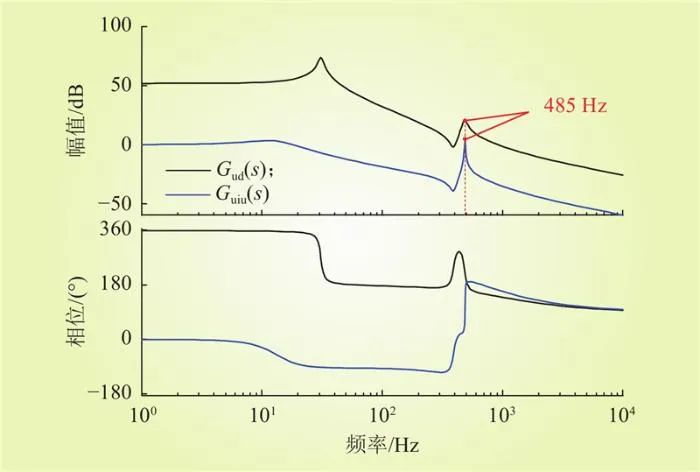
图6 传递函数Gud(s)和Guiu(s)的频域响应曲线(第1组参数)
Fig.6 Frequency domain response curve of transfer functions Gud(s) and Guiu(s) (group 1 parameters)
传递函数Guiu(s)的零极点分布情况如图7所示,从中也可以得到相同的结论。因此,有必要设计出能够抑制该高频振荡尖峰的虚拟惯性参数。
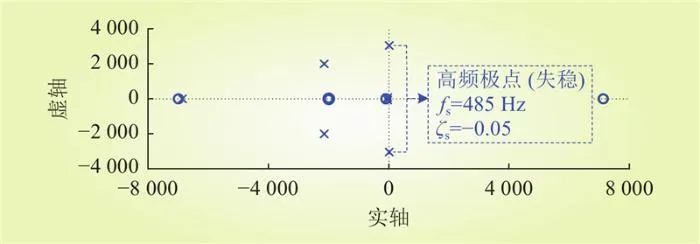
图7 传递函数Guiu(s)的零极点分布(第1组参数)
Fig.7 Zero pole distribution of transfer function Guiu(s) (first set of parameters)
由上述分析可知,可以将高频共轭极点的阻尼比作为判别直流微电网是否发生高频振荡失稳以及虚拟惯性参数是否合理的依据。
2.3 虚拟惯性参数可行域
为明确虚拟惯性参数的可选取范围,本文提出了以下垂系数和低通滤波控制带宽为参数空间的虚拟惯性参数可行域的概念以及基于高频共轭极点阻尼比的虚拟惯性参数可行域求解方法,刻画流程如图8所示。其中,Kdmin和Kdmax分别为下垂系数的最小值和最大值;ωfmin和ωfmax分别为低通滤波控制带宽的最小值和最大值;a和b均为中间变量;x为采样点数。
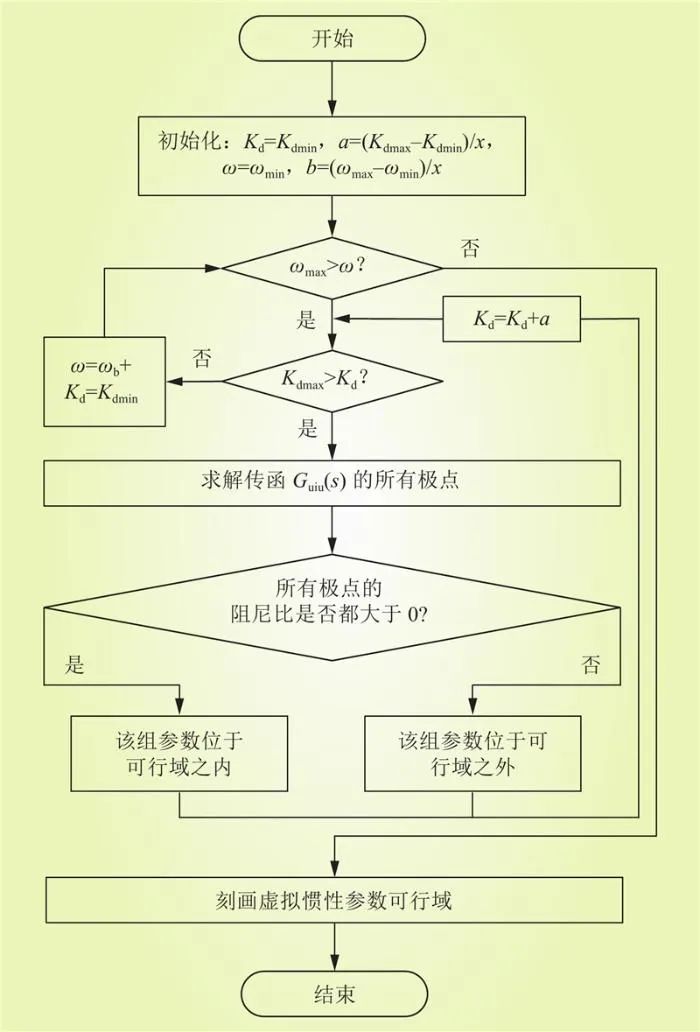
图8 虚拟惯性参数可行域刻画流程
Fig.8 Flow for characterizing the feasible region of virtual inertia parameters
由图8可知,虚拟惯性参数可行域刻画流程可总结为以下4个步骤。
1)输入参数:降阶模型的下垂系数的设定范围为[Kdmin, Kdmax],低通滤波控制带宽的设定范围为[ωfmin, ωfmax],采样点数为x。
2)初始化:下垂系数Kd = Kdmin,步长a = (Kdmax – Kdmin)/x;低通滤波控制带宽ωf = ωfmin,步长b = (ωfmax – ωfmin)/x。
3)判断稳定性:求解闭环传递函数Guiu(s)的零极点,判断高频共轭极点的阻尼比是否为正值。若为正值,则该组参数位于虚拟惯性参数可行域之内;反之,则该组控制参数位于虚拟惯性参数可行域之外。
4)输出虚拟惯性参数可行域:以下垂系数Kd和低通滤波控制带宽ωf为参数空间刻画虚拟惯性参数可行域。
利用本文提出的求解方法刻画该直流微电网的虚拟惯性参数可行域如图9所示。在此基础上,为设置对照,在可行域中选取了4组虚拟惯性参数,如表1所示。不失一般性,在不同的直流微电网中,直流线路的长度也不尽相同。为此,以文献[10]中的线路参数为基准值,直流线路长度分别为1倍长度、1.5倍长度和2倍长度时,虚拟惯性参数可行域分别为VOABCD、VOAEFD和VOAGCD。可以看出,随着直流线路长度的增加,虚拟惯性参数可行域的面积不断扩大;第1组虚拟惯性控制参数(Kd=0.52、ωf=7000rad/s)位于虚拟惯性参数可行域VOABCD之外,即第1组虚拟惯性控制参数不合理。
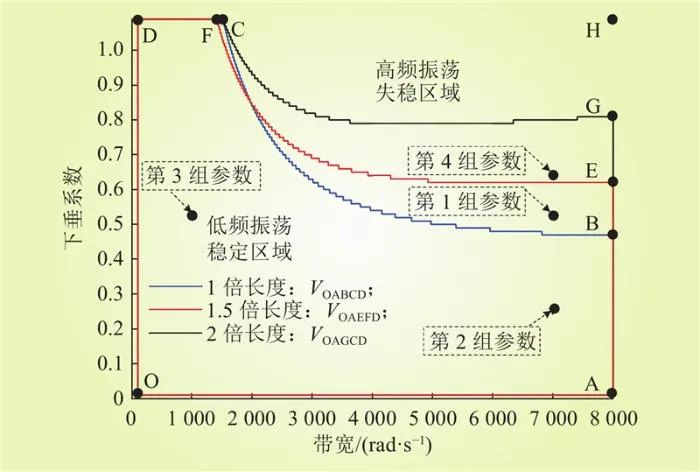
图9 虚拟惯性参数可行域
Fig.9 The feasible region of virtual inertia parameters
表1 4组虚拟惯性参数
Table 1 Four sets of virtual inertia parameters
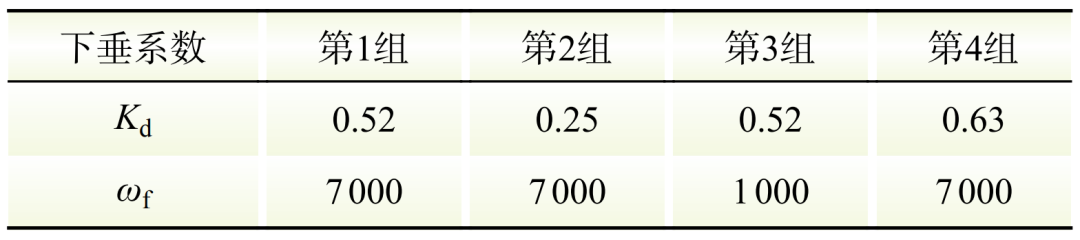
根据虚拟惯性参数可行域选定合适的下垂系数Kd和低通滤波控制带宽ωf后,计算得到第m台DC/DC变换器的下垂系数Kdm和低通滤波控制带宽ωfm为

3 理论分析
3.1 基于虚拟惯性参数可行域的下垂系数设计
由图9可知,第2组参数(Kd=0.25、ωf=7000rad/s)位于虚拟惯性参数可行域VOABCD之内,即第2组参数可有效保证直流微电网的小扰动稳定性。根据图10所示的频域响应曲线可知,第2组参数的高频振荡尖峰要明显小于第1组参数。同时,进行了如图11所示的扫频验证。由图10可知,第2组参数时,传递函数Guiu(s)的理论结果与其扫频结果在低频、中频和高频范围内均几乎吻合,验证了传递函数Guiu(s)低频、中频和高频范围内的精度。
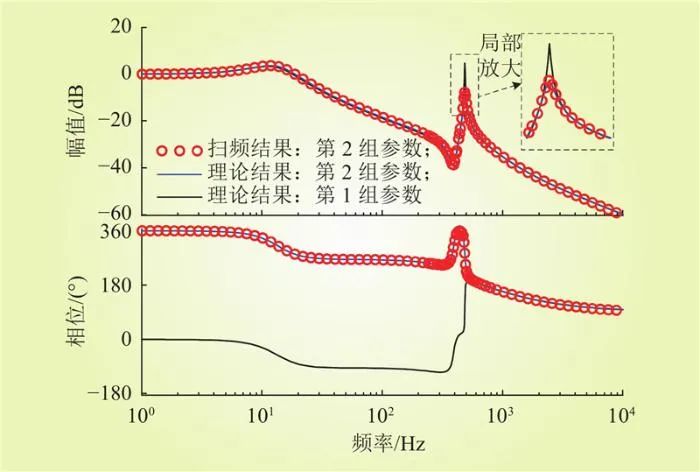
图10 第2组参数的频域响应曲线
Fig.10 Frequency domain response curve of the second set of parameters
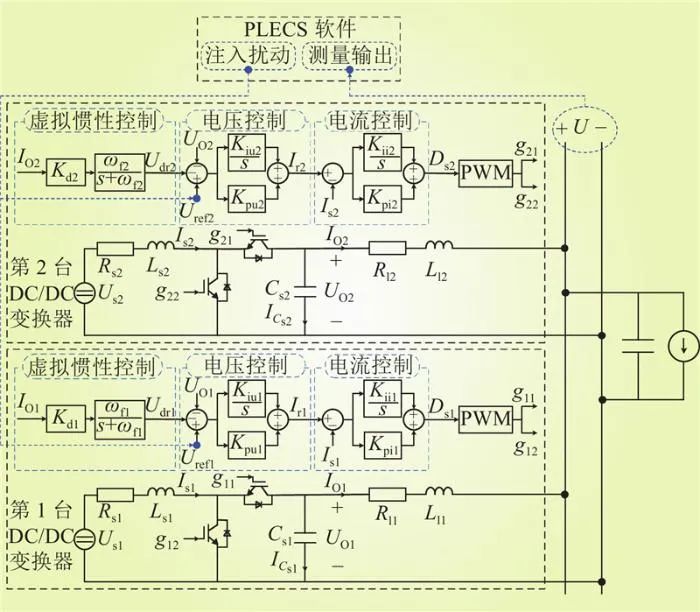
图11 传递函数Guiu(s)的扫频原理
Fig.11 The swept principle of the transfer function Guiu(s)
第2组参数的传递函数Guiu(s)零极点分布情况如图12所示。高频共轭极点的阻尼比为0.02>0,即直流微电网不会出现高频振荡失稳问题,低频共轭极点的振荡频率和阻尼比分别为13.5 Hz和0.444。
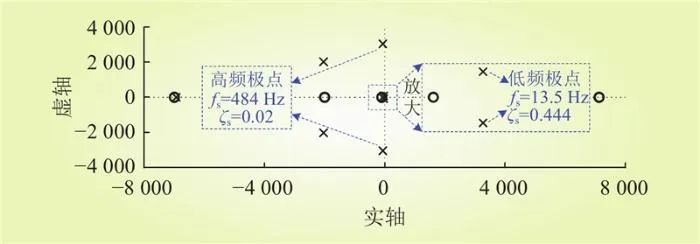
图12 第2组参数的零极点分布
Fig.12 Zero pole distribution of the second set of parameters
3.2 基于虚拟惯性参数可行域的低通滤波控制带宽设计
同理,从图9可以看出,第3组参数(Kd=0.52、ωf=1000rad/s)位于虚拟惯性参数可行域VOABCD之内,即第3组参数也能保证直流微电网的小扰动稳定性。第3组参数的频域响应曲线如图13所示。由图13可知,相较于第1组参数,第3组参数有效抑制了高频振荡尖峰。
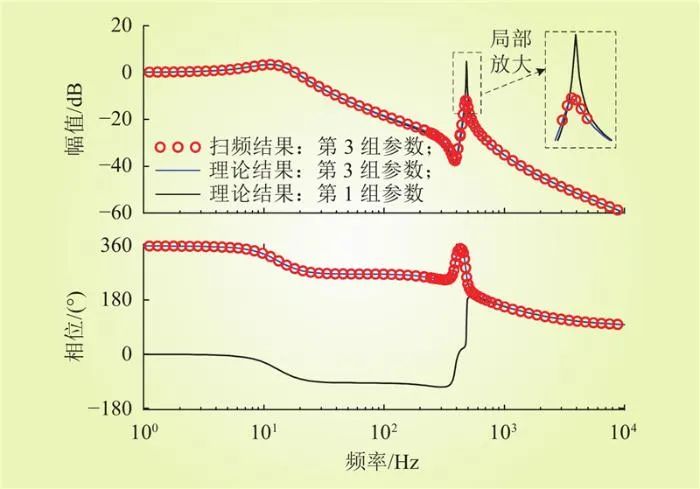
图13 第3组参数的频域响应曲线
Fig.13 Frequency domain response curve of the third set of parameters
第3组参数的零极点分布如图14所示。由图14可知,第3组参数的高频共轭极点位于虚轴左侧,并且低频共轭极点的振荡频率及阻尼比分别为13.2 Hz和0.462,即选取第3组参数时直流微电网呈现低频动态稳定。
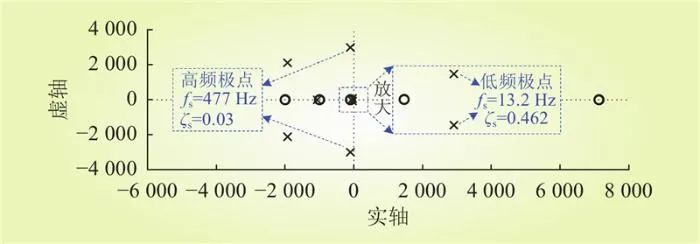
图14 第3组参数的零极点分布
Fig.14 Zero pole distribution of the third set of parameters
3.3 不同直流线路长度的下垂系数设计
从图9可以看出,对于2倍长度直流线路的直流微电网,第4组参数(Kd=0.63、ωf=7000rad/s)是合理的。然而,该组参数却会导致1.5倍长度直流线路的直流微电网出现高频振荡失稳问题。图15为第4组参数的频域响应曲线。由图15可知,第4组参数能够有效抑制2倍长度直流线路的高频振荡尖峰,但却难以抑制1.5倍长度直流线路的高频振荡尖峰。
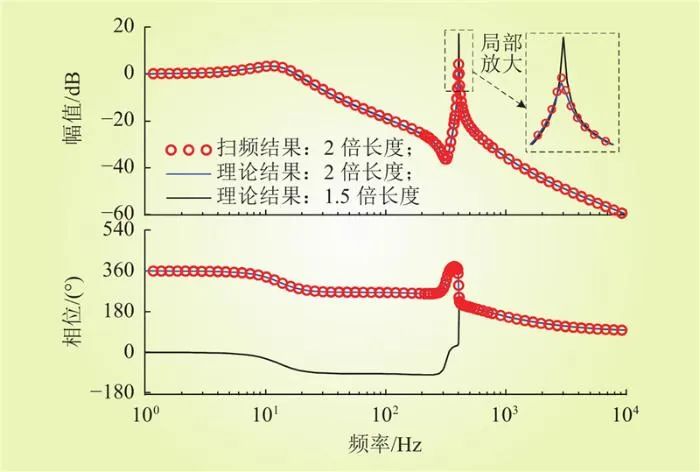
图15 第4组参数的频域响应曲线
Fig.15 Frequency domain response curve of the fourth set of parameters
图16为第4组参数的零极点分布。由图16可知,1.5倍长度直流线路的高频共轭极点位于虚轴的右侧,这就说明直流微电网将出现振荡频率约为404 Hz的高频振荡失稳现象。然而,2倍长度直流线路的高频共轭极点位于虚轴左侧,并且低频共轭极点的振荡频率和阻尼比分别为13.2 Hz和0.458,这说明第4组参数能够保证2倍长度直流线路的直流微电网小扰动稳定性。
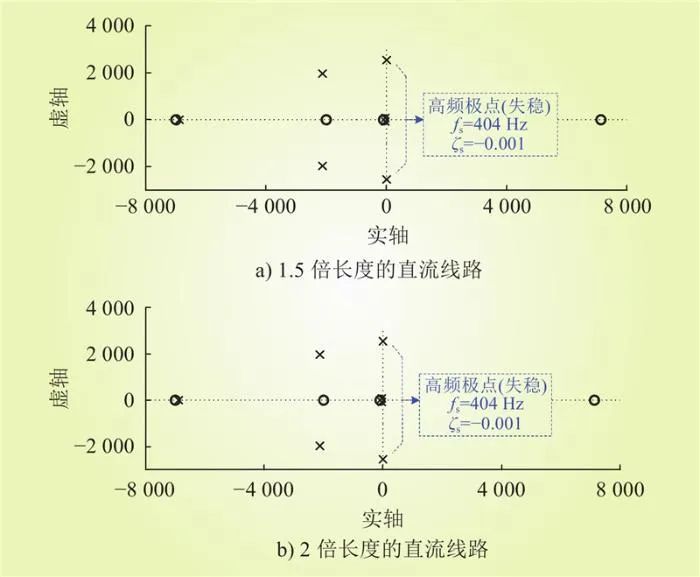
图16 第4组参数的零极点分布
Fig.16 Zero pole distribution of the fourth set of parameters
4 仿真验证
4.1 基于虚拟惯性参数可行域的下垂系数
图17为第2组参数的时域仿真结果。由图17可知,相同扰动场景(0.8 s时,恒功率负荷的功率从0.7 kW突增至1.4 kW)下直流母线电压低频动态过程的振荡频率约为12.6 Hz,与图12中振荡频率理论值(13.5 Hz)基本一致,验证了图9中虚拟惯性参数可行域在下垂系数维度的有效性。
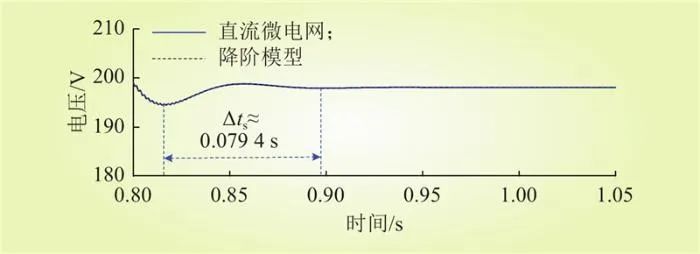
图17 第2组参数的时域仿真结果
Fig.17 Simulation results for the second set of parameters
4.2 基于虚拟惯性参数可行域的低通滤波控制带宽
图18为第3组参数的时域仿真结果。由图18可知,相同扰动场景下,直流母线电压低频动态过程的振荡频率约为11.9 Hz,与图14中振荡频率理论值(13.2 Hz)基本一致。
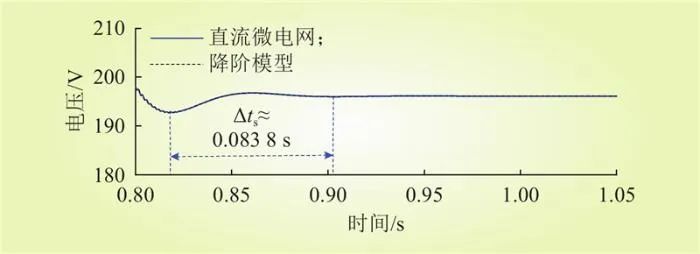
图18 第3组参数的时域仿真结果
Fig.18 Simulation results for the third set of parameters
4.3 不同直流线路长度时的下垂系数
图19为1.5倍和2倍长度直流线路时第4组参数的时域仿真结果。由图19可知,相同扰动工况下,1.5倍长度的直流线路时,直流微电网出现了振荡频率约为400 Hz(振荡周期约为0.0025s)的高频振荡失稳现象,与图16 a)中振荡频率理论值(404 Hz)基本一致。2倍长度直流线路的时域仿真结果呈现低频动态稳定,时域结果中的低频振荡频率约为11.7 Hz,与图16 b)中振荡频率理论值(13.2 Hz)基本一致。上述仿真结果验证了图9中虚拟惯性参数可行域在线路变化时的有效性。
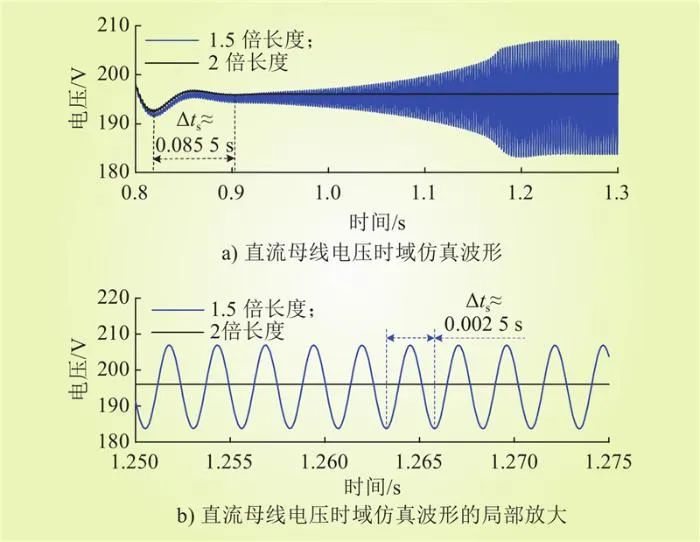
图19 不同长度直流线路的仿真结果
Fig.19 Simulation results for different lengths of DC lines
5 结论
针对虚拟惯性控制参数不合理造成的直流微电网高频振荡失稳问题,本文提出了低通滤波器等效建模方法、虚拟惯性参数可行域的概念及求解方法,主要结论如下。
1)针对包含n台DC/DC变换器的直流微电网(其模型阶数为6n+1阶),提出了低通滤波器等效建模方法,建立了模型阶数为7阶的降阶模型,并推导了降阶模型的电压闭环传递函数,多组仿真结果验证了该降阶模型的有效性。
2)针对不合理虚拟惯性控制参数引发的直流微电网高频振荡失稳问题,定义了以下垂系数和低通滤波控制带宽为参数空间的虚拟惯性参数可行域的概念,并提出了基于高频共轭极点阻尼比的虚拟惯性参数可行域求解方法。基于所刻画的可行域,能够设计出有效保证直流微电网小扰动稳定性的下垂系数和低通滤波控制带宽。
3)保持低通滤波控制带宽(或下垂系数)不变时,减小下垂系数(或低通滤波控制带宽)能够有效避免直流微电网出现高频振荡失稳问题,即有效提高直流微电网的小扰动稳定性。
一方面,在此虚拟惯性参数可行域基础上,如何量化设计低通滤波控制带宽,使得直流母线电压的时域仿真波形呈现出理想虚拟惯性特征,值得未来深入探讨;另一方面,针对由不同参数DC/DC变换器构成的直流微电网,如何开展虚拟惯性控制参数设计,也是未来的研究方向之一。
注:本文内容呈现略有调整,如需要请查看原文。